NN:one neuron

Simple Neuron

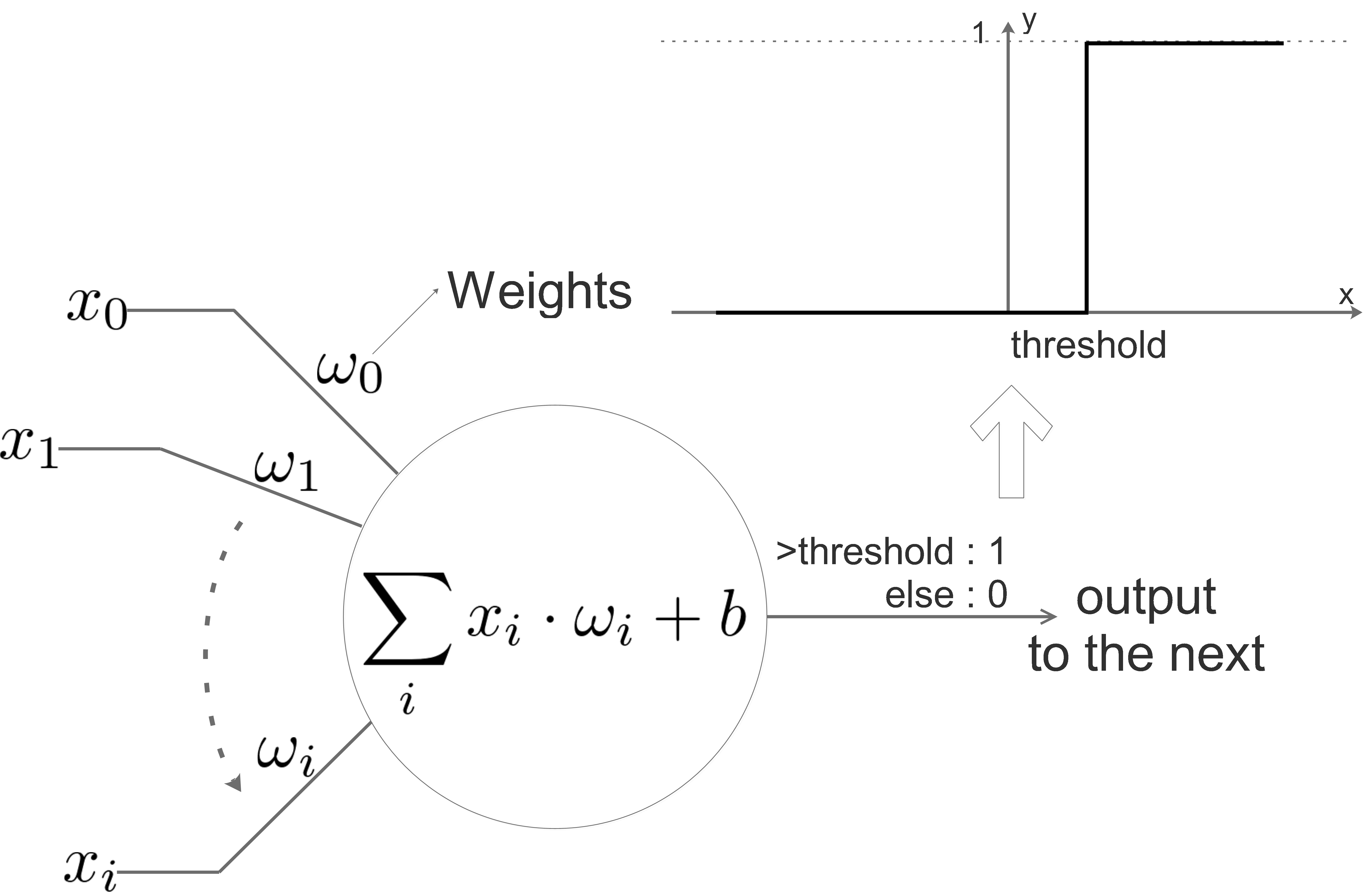
The above diagram shows a neuron in NN, it simulates a real neuron:

it has inputs: \(x_{0},x_{1}\dots x_{i}\)

it has weights for each inputs: \(\omega_{0},\omega_{1}\dots \omega_{i}\): weight vector

it has bias \(b\)

it has a threshold for the “activation function”

The neuron process the inputs with the equation inside the circle, if the result is bigger than the threshold, the neuron will not be activated and output 0, if the result if bigger than the threshold, the neuron will be activated and output 1.

We can consider a neuron as a binary classifier.

Practical Thinking

Sometimes we choose the activation function as \(Max(0,\omega \cdot x+b)\):

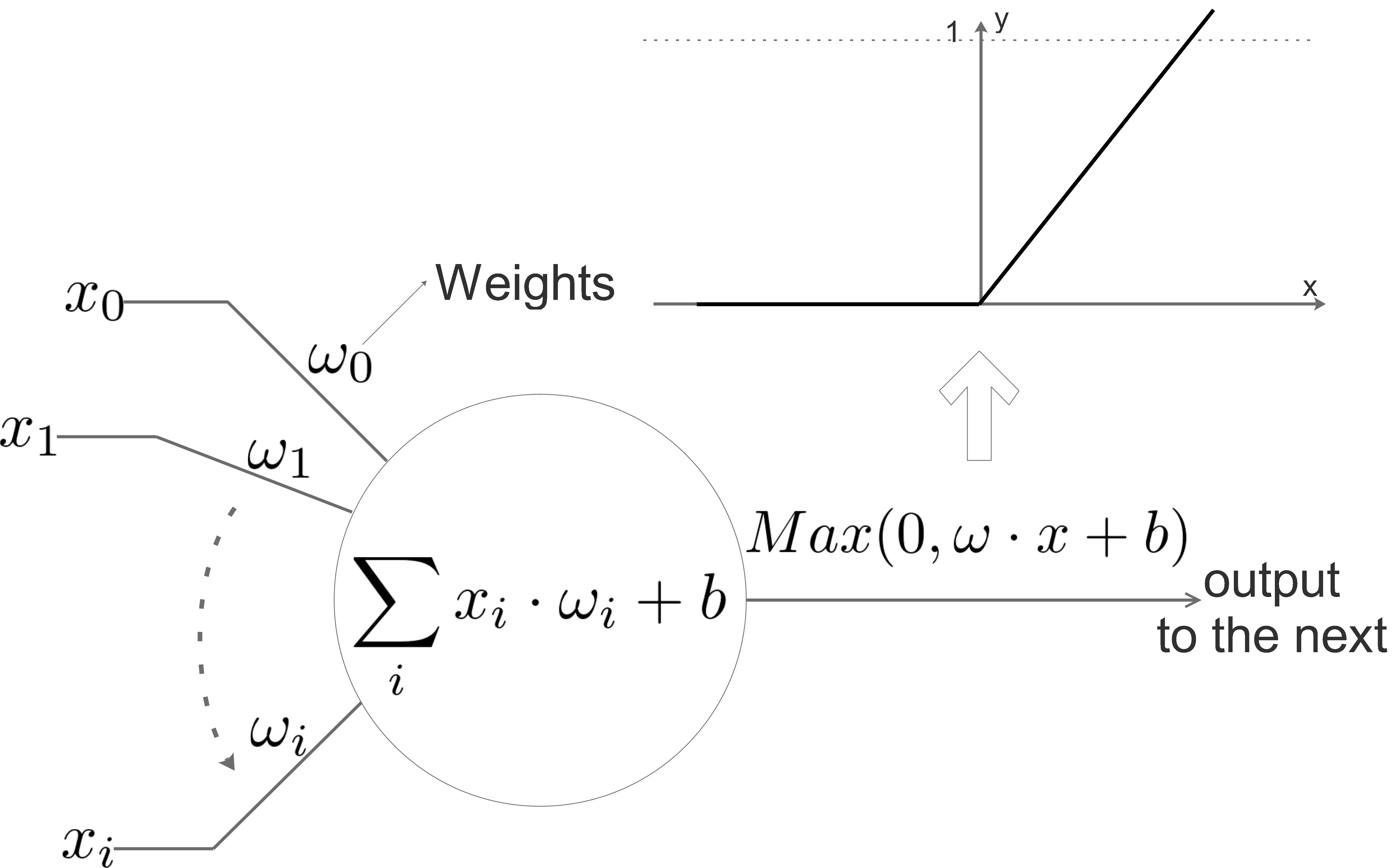
Let’s make it a practical case:

\(x\) is a 3072x1 feature vector, then for this neuron,

\(\omega\) is a 1x3072 weights vector,

\(b\) is a real value bias.

If we have 100 neurons on the 1st layer, they get the same input \(x_{0},x_{1}\dots x_{i}\) with different weight vectors. We can combine all these 100 neurons to one big weight matrix \(W_1\), its size is 100x3071, each row of \(W_1\) is a weights vector of a neuron, so the output of the 1st layer will be a 100x1 output vector: each neuron outputs one value. It means the information is extracted and the dimension of the information is reduced from 3071 to 100. The equation for the 1st layer will be:

$$Max(0,W_1\cdot x + b_1)$$:output a 100x1 vector

Now we add the 2nd layer, we set it to be 10 neurons, then it will receive the 100 inputs and output 10 inputs, combining the 1st and the second layer:

$$Max(0,W_2\cdot Max(0,W_1\cdot x + b_1) + b_2)$$:output a 10x1 vector

\(W_2\) is a 10x100 weights matrix, it contains all the computation of the 2nd layer, each row of \(W_2\) is a weights vector of a neuron in the 2nd layer. \(b_2\) is the 10x1 bias vector of the 2nd layer.

Of course we can add the 3rd, 4th layers and so on, then the whole NN can be represented as a chain of activation functions:\(Max(0,-)\) .

More possibilities of Activation Function

Sigmoid

Previously, we usually use sigmoid function \(\frac{1}{1+e^{-x}}\) as activation function:

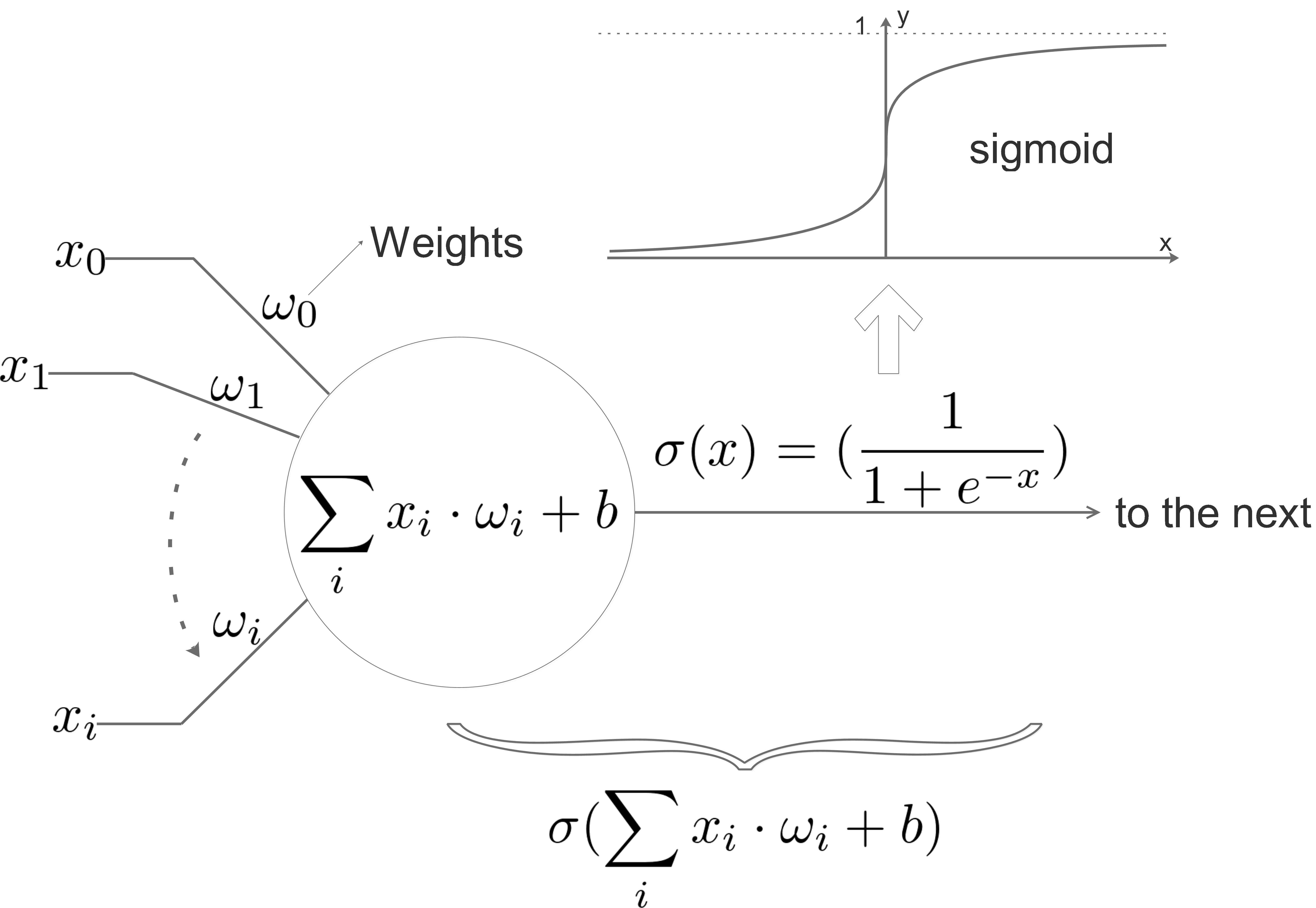
One reason to use this function is because it’s differentiable, we will use gradient descent to train the NN, we need the activation function to be differentiable.

Another reason is because this function always output a value between 0 and 1.

And it can be explained physically: its output value can be understood as a possibility:

$$\sigma(\sum_ix_i\cdot \omega_i+b)=P(y_i =1\vert x_i;\omega)$$

Using regularization, we may notice that the \(\omega\) gets smaller when the training process goes on, it can be explained as forgetting: the \(\omega\) turns smaller means the information in each neurons is weaker, which means the NN is forgetting.

The 3rd reason is historical ….

But it is rarely used now, it has the following drawbacks:

1, When \(x\rightarrow\infty\), the sigmoid’s gradient is almost 0, the same thing happens when \(x\rightarrow-\infty\). During the back propagation, if \(\omega\) is very big(may be initialized this way), gradient will be very small, then the update in every training iteration will be very tiny:it doesn’t update at all, the learning efficiency will be very low.

2, sigmoid function always outputs positive value, during the back propagation, the gradient of \(\omega\) is either all positive or negative, which brings a zig-zag dynamics, this is also of low efficiency.

Tanh

In order to improve the sigmoid, Tanh is invented, it uses the sigmoid’s nonlinearity, actually it is a scaled sigmoid:

\[Tanh(x) = 2\sigma(2x)-1\]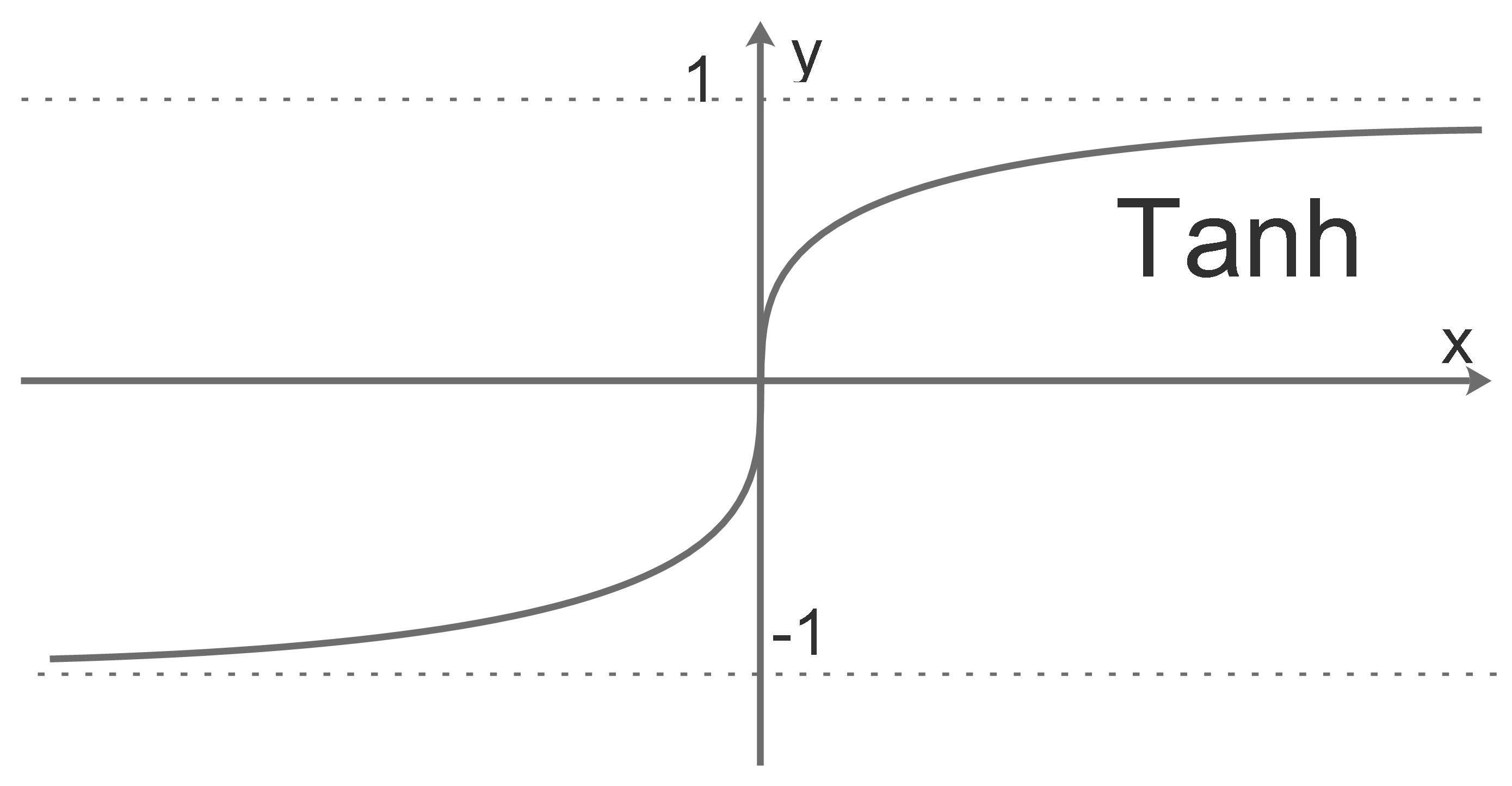

Obviously, it overcomes the sigmoid’s 2nd drawback.

ReLU

The Rectified Linear Unit(ReLU) is another alternative, this is the one we used in “Practical Thingking”, it’s simple:

$$f(x)=max(0,x)$$ combining the neuron: $$f(x) = Max(0,\omega\cdot x+b)$$

Pro:

1, Computing cost is very low, simple thresholding, relative to sigmoid’s exponentials.

2, Very fast convergence using stochastic gradient descent

Con:

It may die after some updates, the neuron may be always deactivated and output 0. Why? Take a look at the following diagram:

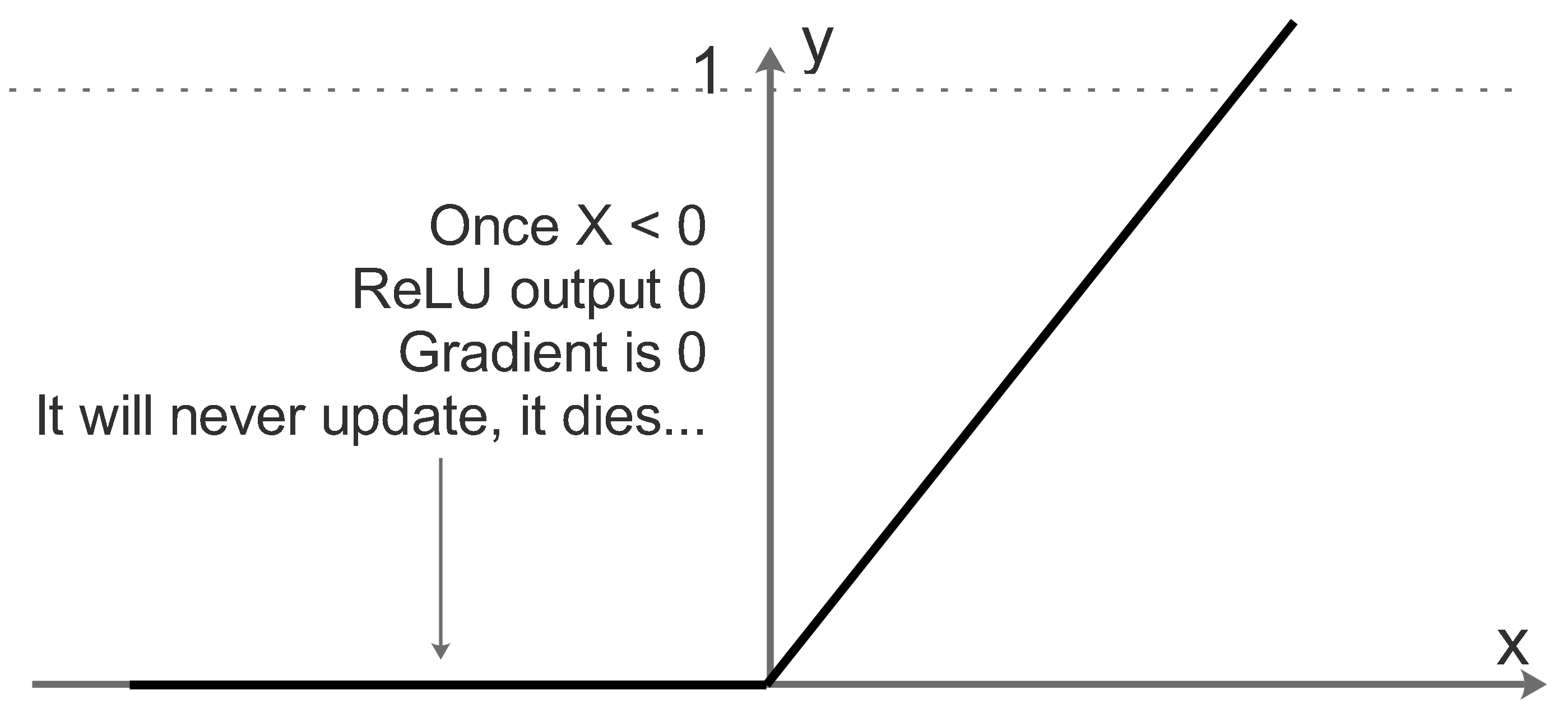
Leaky ReLU

In order to overcome the drawback of ReLU, the Leaky ReLU introduce non-zero:

when \(x<0\:: f(x)=ax\) (\(a\) is a small constant value)

when \(x>0\::f(x)=x\)

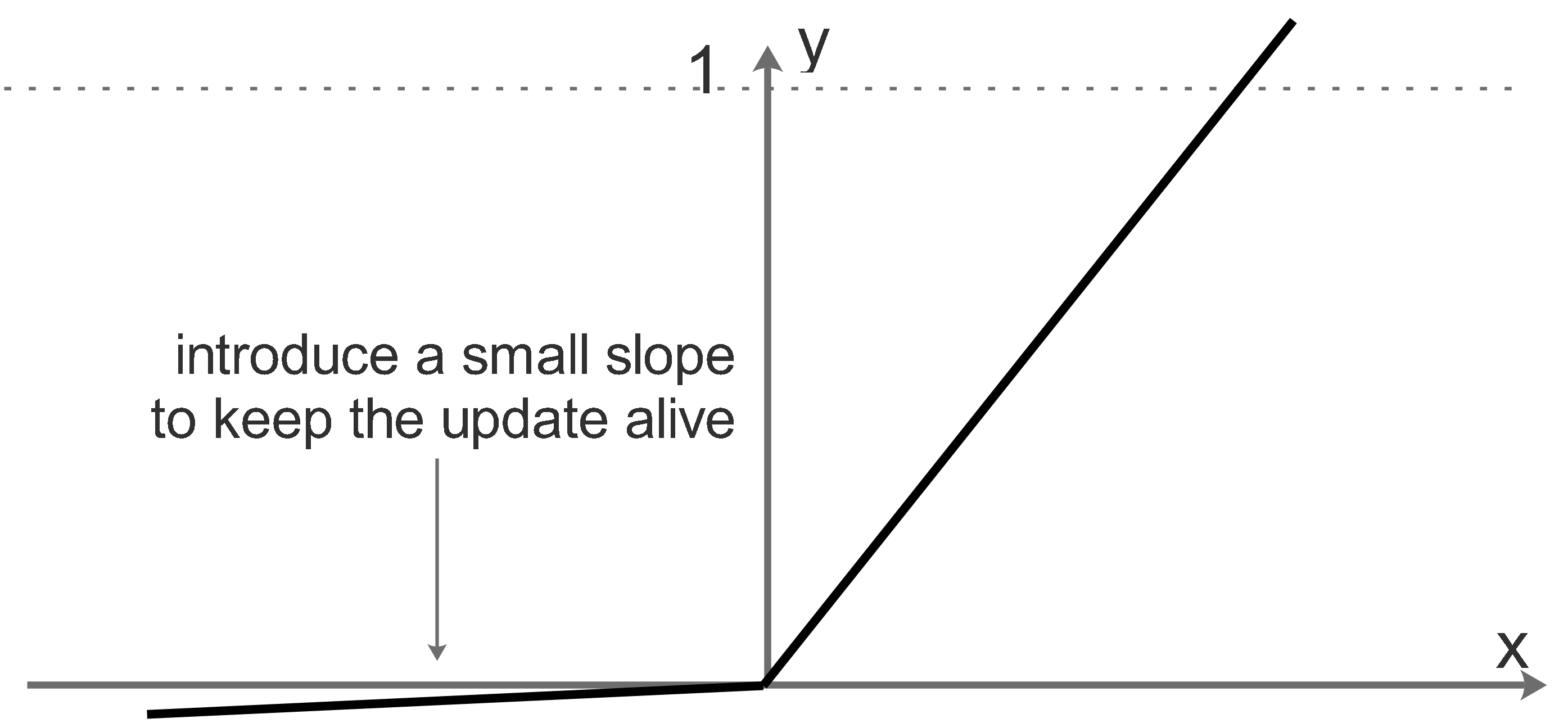
Maxout

Maxout’s idea is not using a fixed activation function but learn one.

A Maxout neuron contains more than 1 \((w,b)\) pairs.

For traditional neuron, we get \(f(x)=\omega\cdot x+b\)

For Maxout neuron, we get

\(f_1(x)=\omega_1\cdot x +b_1\) ,\(f_2(x)=\omega_2\cdot x +b_2\) and \(f_i(x)=\omega_i\cdot x + b_i\).

The final result will be the max of all \(f_i(x)\):

$$Maxout(x)=\displaystyle\max_{i=1\dots k}(f_i(x))=\max_{i=1\dots k}(\omega_i\cdot x + b_i)$$

\(k\) means the Maxout neuron contains \(k\) linear models

The max will win and used as the output, that’s why it is called “Maxout”.

Which Type of Neuron should we use?

We should follow this priority:

Maxout/Leaky ReLU > ReLU > Tanh

Never use Sigmoid