NN Dropout
Dropout regularization
Dropout is a commonly used regularization method, it can be described by the diagram below: only part of the neurons in the whole network are updated. Mathematically, we apply some possibility \(p\)(we use 0.5) to a neuron to keep it active or keep it asleep:
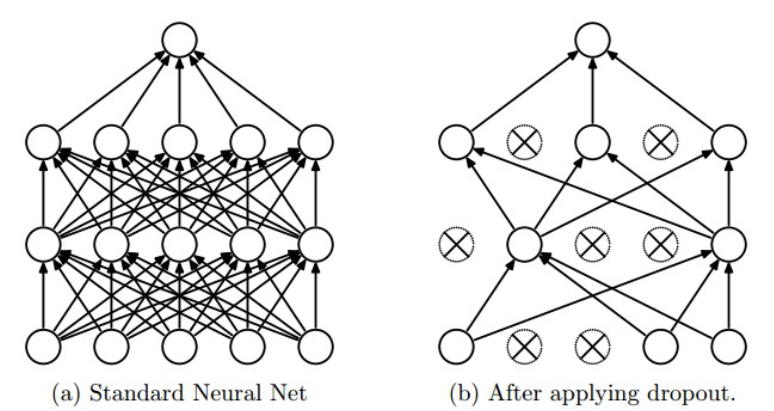
Normally we only apply the dropout regularization to the middle layers, but you can also apply it to the input layer, which means adding a binary mask to the input data.
What’s really important is that we are not dropping out neurons for prediction! It brings a problem: the neurons in prediction phase is respecting the same data as the training phase but it is not, in the training phase neurons only received 50% outputs from the last layer(we use \(p=0.5\)), which means the strength of the input signal of each neuron during the prediction phase is 2 times of the signal in training phase.
So we should reduce the signal strength for prediction: all neurons’ outputs will be scaled by \(p\). Practically:
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X):
""" X contains the data """
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(W1, X) + b1)
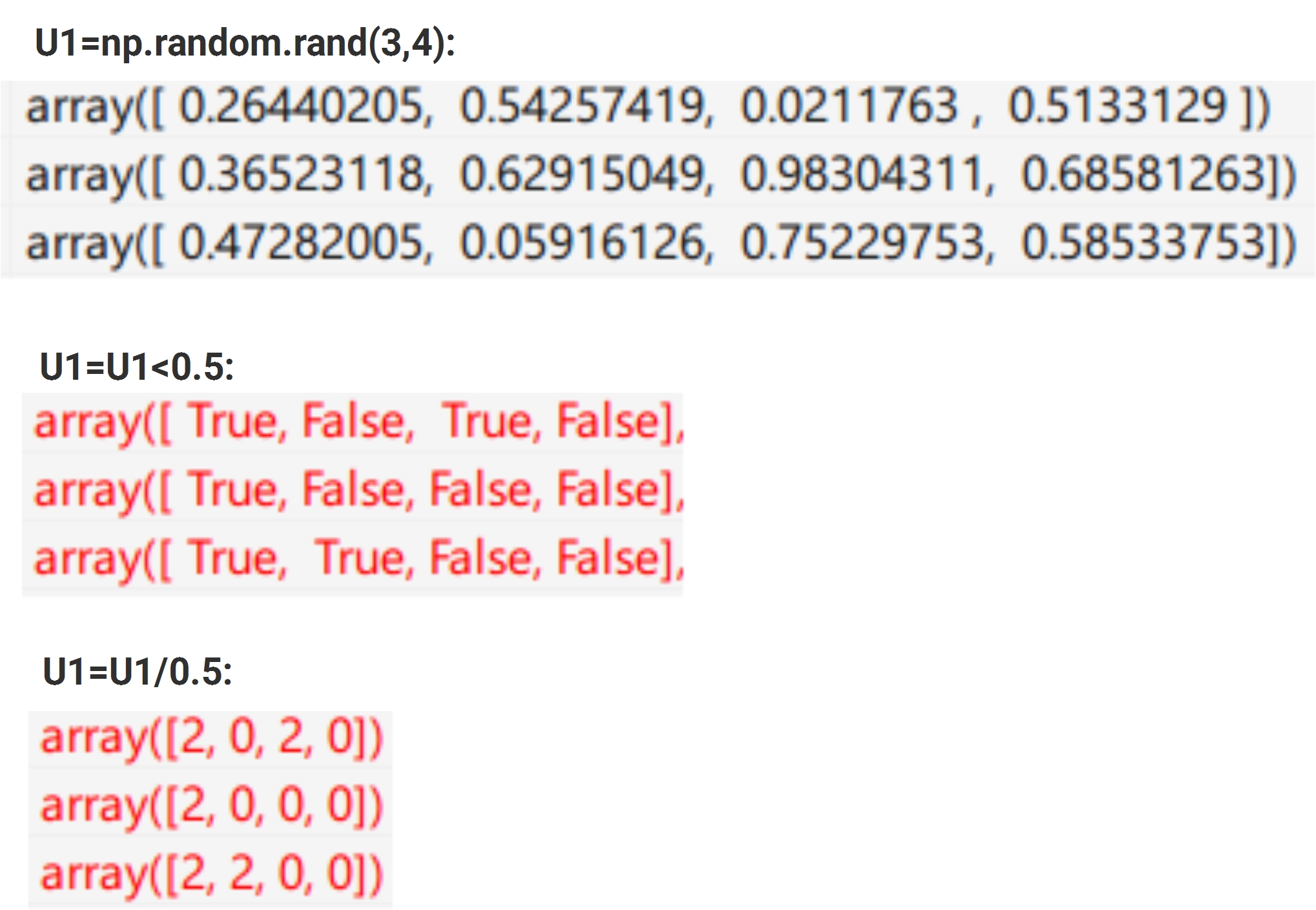
U1 = np.random.rand(*H1.shape) < p # first dropout mask
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = np.random.rand(*H2.shape) < p # second dropout mask
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown)
# perform parameter update... (not shown)
def predict(X):
# ensembled forward pass
H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations
H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
out = np.dot(W3, H2) + b3
As prediction usually has high requirement on performance, we don’t want an additional multiplication after each neuron, so it will be better to put the scaling at training time, which is called inverted dropout:
"""
Inverted Dropout: Recommended implementation example.
We drop and scale at train time and don't do anything at test time.
"""
p = 0.5 # probability of keeping a unit active. higher = less dropout
def train_step(X):
# forward pass for example 3-layer neural network
H1 = np.maximum(0, np.dot(W1, X) + b1)
U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# backward pass: compute gradients... (not shown)
# perform parameter update... (not shown)
def predict(X):
# ensembled forward pass
H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
H2 = np.maximum(0, np.dot(W2, H1) + b2)
out = np.dot(W3, H2) + b3
This is how it works in the program: