Graph Optimization 1 - Modelling Edges and Vertices
- How to model the world
How to model the world
What the vertices and edges really mean in graph-based SLAM?
The graph optimization’s essential idea is modeling the SLAM problem as a graph. The tutorials usually say that the camera’s poses are modeled as a vertex in a graph, the edge connecting two vertices represents a constraint. Which somewhat simplifies the problem and makes the reader confusing.
Because, not only the camera poses can be modeled as vertices, but also 3D landmarks. A constraint is a concept usually used in optimization, for someone who is not familiar with optimization, the edges just represent some physical relationships.
What is edge and vertex in Graph Optimization?
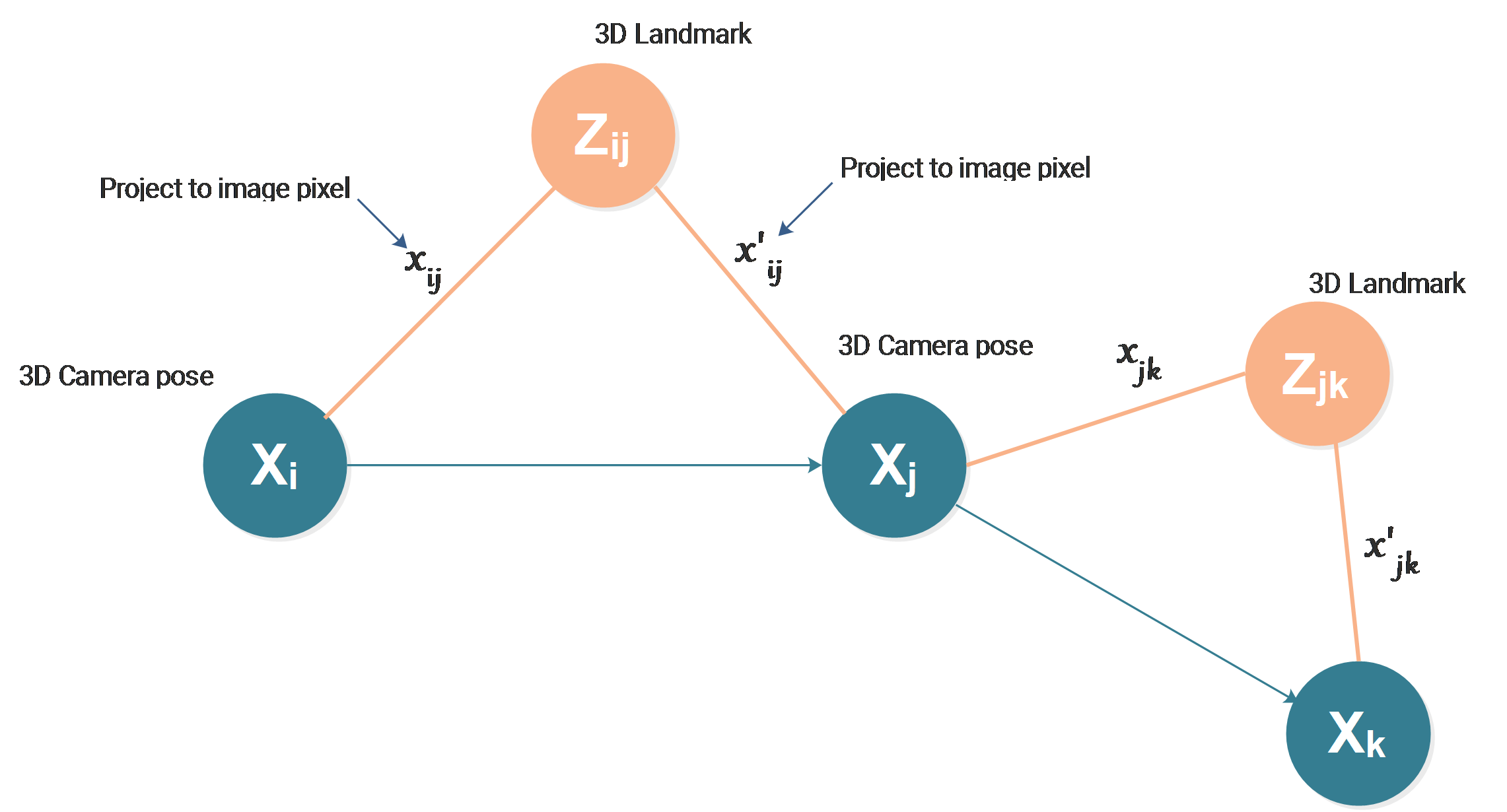
Let us take the above graph as an example, it is actually bundle adjustment represented in the form of a graph.
Vertex
Sometimes it is also called node in graph optimization. In this graph, we can see two kinds of vertices.
Camera Pose Vertices
The cyan vertices represent the camera poses. Even for camera poses, it can also be modeled in many ways according to our needs. For the above case, the camera poses are modeled in the form of \(R,t\) as 3x3 rotation matrix and 3x1 translation vector respectively. In some cases when we only care about location, the camera pose vertices can also be modeled as 3D position as \((x,y,z)\). When dealing with a robot moving indoor, they can even be modeled as 2D position as \((x,y)\) by ignoring the vertical position change.
Landmark Vertices
The orange vertices represent the landmarks. In the case of the above graph, landmarks are modeled as 3D points as \((x,y,z)\). Similar to camera poses, the landmark vertices can also be modeled differently according to the requirements. If we ignore the vertical direction for an indoor robot, the landmark also turns to be 2D positions as \((x,y)\).
Visualization convention: should the vertices aligned along a line?
In the field of robotics, people usually visualize the vertices like the physical position of the camera, but the people that are familiar with probabilistic models may visualize the nodes on a straight line. They are theoretically the same.
Edges
Usually, edges are considered as “constraints” in graph optimization. Practically, it can model different physical relationships between vertices, the constraints can be explained as “estimation targets constrained by real measurements”. So the edge of the graph always means some kind of “measurement”.
Edges between Camera Poses
In some tutorials, the edges between camera poses are usually described as odometry constrains from visual odometry or IMU odometry data. Actually, they are not always needed. For example, in the case of bundle adjustment, we have no measurements between two camera poses, so we don’t have them. The graph turns to be:
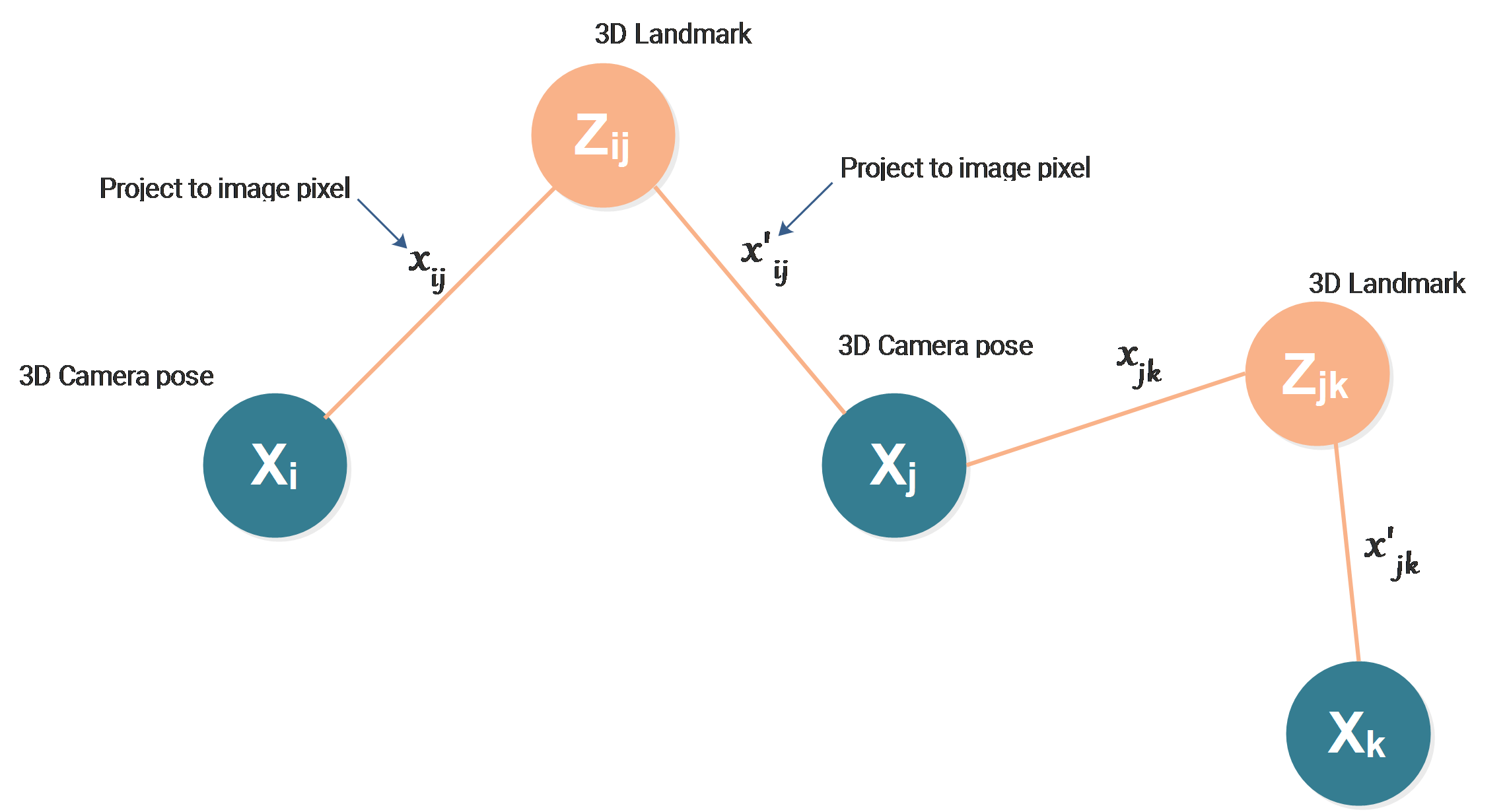
Edges between landmarks and camera poses
The edges between landmarks and camera poses represent the 3D→2D projection as a measurement method, the landmark at position \(Z_{ij}\) is projected to the image pixel \(x_{ij}\) by the camera positioned and oriented at \(X_i\). The pixel position \(x_{ij}\) is then the measurement.
Now we can see that there is always some measurement hidden in the edge connecting two vertices.
For bundle adjustment, we get image pixels as measurements. The position of our estimation targets, our unknown landmarks, and camera poses are constrained by the measurements. The real positions of the landmarks and the cameras must follow the physical rule to give us the measurements we get.
Solving a SLAM problem means estimating the position of landmarks and cameras.
Measurements
In order to solve this problem, we need to measure the world using some measuring devices, based on the measured information, we try to estimate the world hidden behind the measuring devices.
When the robot moves from one position to another, the image taken from the camera on the robot will be different, this difference is caused by the robot’s motion, here we use the camera as the measuring device to measure the camera’s motion and the image is the measurement.
If we also mount an IMU on the robot, the robot’s motion will also be measured by the IMU. There are also other measurement devices, such as GPS, LiDAR, ultrasonic sensor, and Radar sensor.
The measurement we get will never change, this is the only thing we get.
Practically, in the above bundle adjustment case, the image pixel coordinates \(x_{ij},x_{ij}^{'},x_{jk}\) and \(x_{jk}^{'}\) are the measurements we get, they correspond to 4 edges. It can easily be seen that for 2 landmarks and 3 camera poses, we only have 4 image pixels as measurements. We get 4x2 measured values, but on the other hand, we get 2x3 unknowns for landmarks and 3x6 unknowns for camera poses, the measurements are definitely not enough. That’s why we need to take hundreds of image pixels.
Estimations
What we want to get is the landmark and camera positions, for the camera, orientation is also important. The information we want to compute is called estimation, it is always changing.
In a closed-form solution, the unknowns can be solved directly in one step. When using iterative methods, the estimation is always changing in each iteration. We can then stop iterating when the estimation is good enough according to our requirements.
The problem is, how can we know if the estimation is good or bad?
There are many methods to define it. Usually, we need to know the measurements model. The measurements model can generate the measurements based on some given estimation. For example, if we know the poses of the cameras and the positions of the landmarks, we can simulate the measurement process and compute the image pixels’ coordinates based on the measurement model (camera projection model), then we can compare the generated measurements and the real measurements to define if the estimations are good or bad.
Here practically, based on the estimated landmarks and camera poses, we can project the landmarks to the images taken by the cameras and get the projected image pixels, for example:
\[\hat x_{ij}=K[X_{ij}]Z_{ij}\]\(\hat x_{ij}\) is the simulated image coordinates as a 2D projection of the 3D landmark \(Z_{ij}\) onto the image, the pose of the camera is \(X_{ij}\). In the above equation, \(X_{ij}\) is a combination of rotation and translation matrix represented as a 3x4 projection matrix \([R,t]\). \(K\) is the intrinsic matrix of the camera.
Then we can simply compute:
\[e_{ij}^2=(\hat x_{ij}-x_{ij})^2\]as the error between real measurement and simulated measurement based on the current estimation.
