NN Architecture
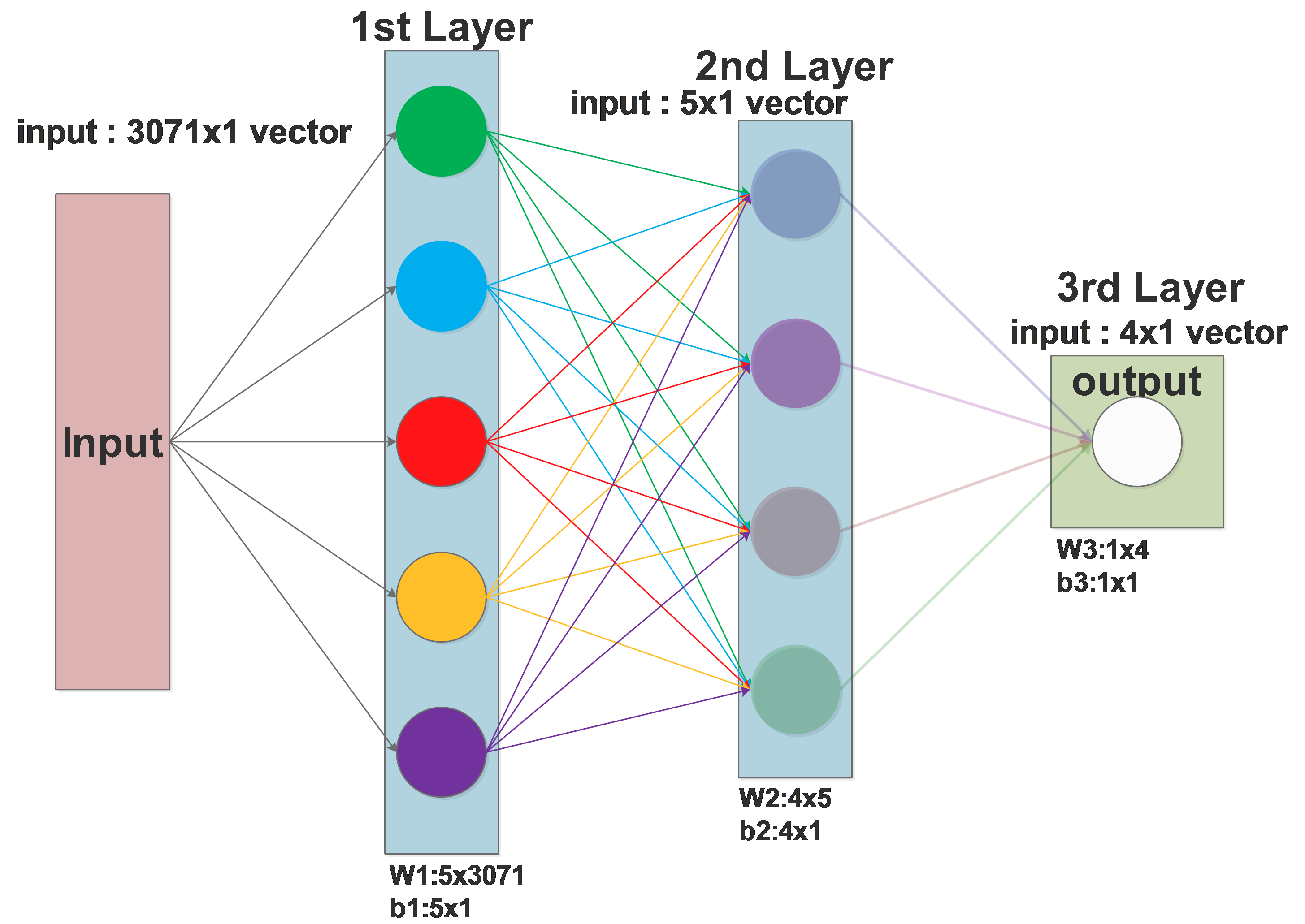
Input: The input feature vector, if we are dealing with image patches, it will be long
Layers: One layer is constructed by many neurons, a neuron is a combination of a linear classifier and a activation function:
\(x\) is a 3071x1 vector, \(\omega\) of one neuron is a 1x3071 weights vector, \(b\) is a real value.
So one neuron in the 1st layer outputs one single value(marked by one color), this value will be copied to all the neurons of the 2nd layer.
The 1st layer, consist of 5 neurons, will output a 5x1 vector to the 2nd layer.
Then all the neurons in the 2nd layer will receive the same 5x1 vector from the the 1st layer as their inputs.
We can see that the original input, a 3071x1 vector is now compressed to a 5x1 vector by the 1st layer.
Or we can describe it more accurately: each neuron of the 1st layer extracts some key information from the 3071x1 input vector, all 5 neurons extracted 5 different kinds of information and store them in a vector.
The 2nd layer will further extract 4 kinds of information out of the 5x1 information vector from the 1st layer and output a 4x1 vector to the 3rd layer, the 3rd layer will output 1 value as the final result.
Mathematically
We can represent each layer as one weights matrix:
input \(x\): 3071x1
1st layer \(W_1\) : 5x3071, \(b_1\) : 5x1
2nd layer \(W_2\) : 4x5, \(b_2\) : 4x1
3d layer \(W_3\) : 1x4, \(b_3\) : 1x1
The equation after the 1st layer will be:
\[F(x)=Act(W_1\cdot x+b_1)\]after the 2nd layer:
\[F(x)=Act(W_2\cdot Act(W_1\cdot x+b_1)+b_2)\]after the 3rd layer:
\[F(x)=Act(W_3\cdot Act(W_2\cdot Act(W_1\cdot x+b_1)+b_2)+b_3)\]The above equation describes the whole NN
Practically
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (sigmoid)
x = np.random.randn(3071, 1) # random input vector(3071x1)
h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer activations (5x1)
h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1)
out = np.dot(W3, h2) + b3 # output neuron (1x1)
Or we can put all together:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (sigmoid)
x = np.random.randn(3071, 1) # random input vector(3071x1)
out = np.dot(W3,f(np.dot(W2,f(np.dot(W1, x) + b1) ) + b2) )+b3
