NN Softmax loss function
Background:the network and symbols
Firstly the network architecture will be described as:
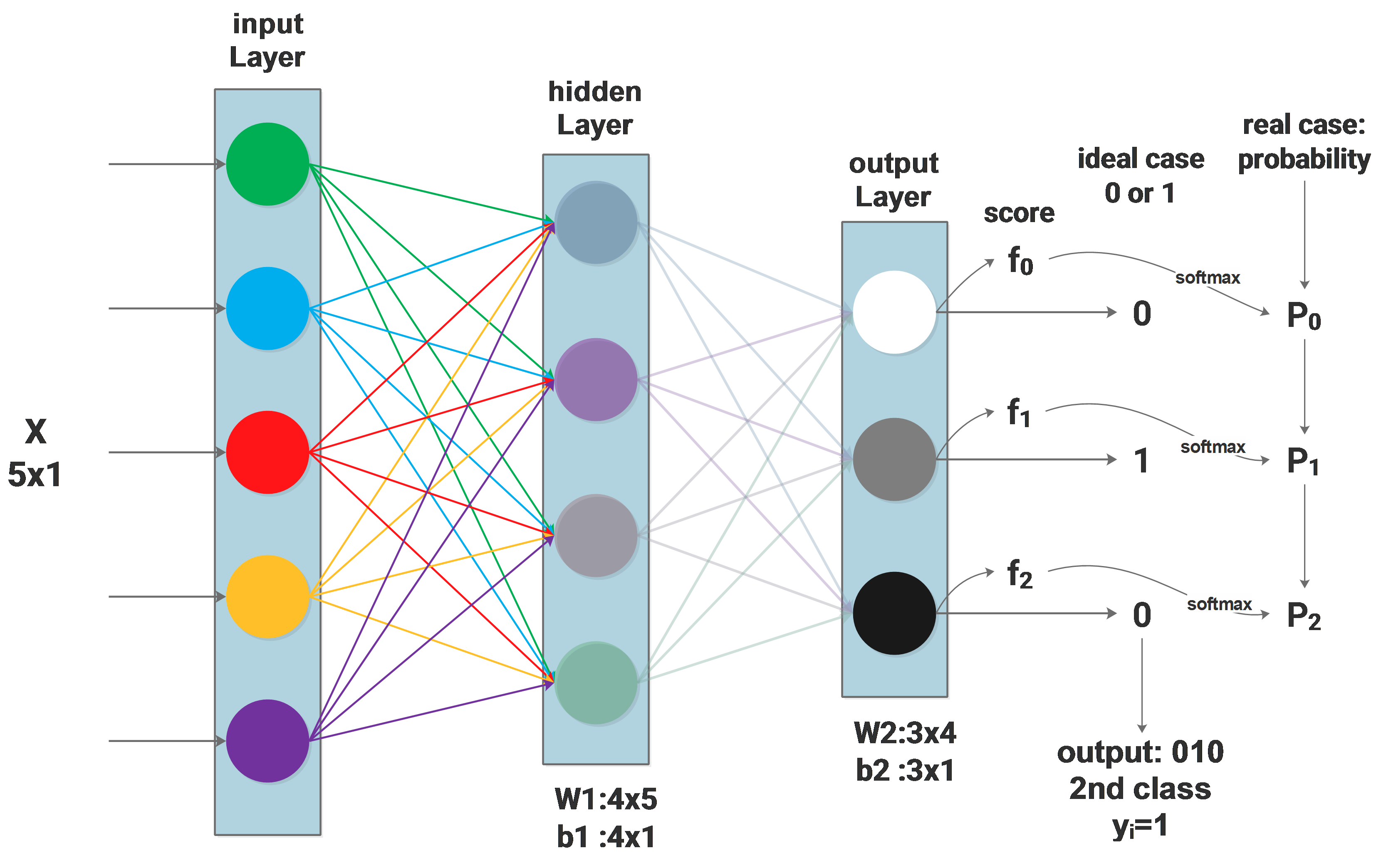
We are now dealing with a multi-class classification problem, let’s say there are 3 classes, then the output layer has 3 neurons, each neuron output a binary value, the neuron outputs 1 will be the target class, the other neurons output 0, as our target is one single class. The so called “ideal” case is the ground truth from the training set. For the ith sample from the training set, it will be represented as <\(\scriptsize X_i,y_i\)>, \(\scriptsize X_i\) is a feature vector and \(y_i\) means its class. The sample in the above diagram belongs to the 2nd class, then the value of \(y_i\) will be 1(index from 0) and the 3 neurons of the output layer will output 0,1,0 respectively.
Obviously, for the given input \(\scriptsize X_i\) we can hardly get an output of absolute 1 or 0, instead, after a complicated data flow from the input layer till the output layer, what we get from the output layer directly will be some scores, which are \(f_0,f_1,f_2\) from 3 neurons, their range can be anything, depending on the W and b through the whole network, they are computed by:
\[f=W\cdot X+b\]Softmax function
The softmax function will be:
\[P_i=\frac{e^{f_{y_i}}}{\sum\limits_{j=0}^{C=2}e^{f_j}}\\\]symbols:
\(\scriptsize X_i\) : input feature vector, with a length of 5 in this case
\(y_i\) : output value, ground truth from the training set, can be 0, 1 and 2
N : number of samples in the training set
\(\scriptsize i\) : the \(i^{th}\) sample
\(\scriptsize f_j\) : output score, can be \(\scriptsize f_0,f_1,f_2\)
\(\scriptsize j\) : the \(j^{th}\) class
C : number of classes, in this case 3
\(\scriptsize P_j\): probability of the \(j^{th}\) output to be the correct class
we can see that the range of \(\scriptsize P_j\) will always be [0,1], which will be considered as the probability of the output to be the \(y_i^{th}\) class(classified correctly), its ideal case is 1: 100% for sure belongs to the \(y_i^{th}\) class.
Softmax function is actually a bridge connecting the direct outputs and the final result: the class with the biggest probability is the predicted class.
Define the Loss function
Now we have the training set containing some \(\scriptsize <X,y>\) pairs.
We are looking for the network parameter matrix \(\scriptsize W\), which can be described as:
\[arg\max_W{P(W|X,y)}\]As \(\scriptsize <X,y>\) is given, \(\scriptsize P(X,y)\) will be 1 and \(\scriptsize P(W)\) is considered to be some constant. Using the Bayes’ theorem, the initial problem turns to:
\[arg\max_W{P(X,y|W)}\]given W, we get the output scores \(f\) from X, so the problem turns further to:
\[arg\max_W{P(f,y|W)}\]using the joint probability:
\[P(f,y|W)=P(y|f,W)\cdot P(f|W)\]what’s more
\[P(f|W)=P(X)\cdot P(W)\]and both probabilities of the right side are constant, so finally our problem turns to:
\[arg\max_WP(y|f,W)\]which can be described as follows:
given a network and the input \(\scriptsize X\) from the training set , looking for a \(\scriptsize W\), which can maximize the probability of the \(\scriptsize X\)’s correct classification: \(y\)
As discussed above, this probability can be expressed with the softmax function. Putting all training samples together, we get:
\[arg\max_W\prod_{i}^{N}\frac{e^{f_{y_i}}}{\sum\limits_j^Ce^{f_j}}\]log it, we get:
\[arg\max_W\sum_i^Nlog(\frac{e^{f_{y_i}}}{\sum\limits_j^Ce^{f_j}})\]normally the optimization problem aims to minimize something, we add a minus and get the final loss function:
\[\mathscr{L}=arg\min_W\sum_i^N-log(\frac{e^{f_{y_i}}}{\sum\limits_j^Ce^{f_j}})\]First step of optimization: calculate the derivative
The backpropagation algorithm will be discussed in the next blog, I’d like to introduce the first step: calculate \(\frac{\mathscr{dL}}{\mathscr{d}f}\).
start from the above \(\mathscr{L}\), through a serious of calculation, the derivative of the loss to the \(f\) to the correct outputs will be:
\[\frac{\mathscr{dL}_{y_i}}{\mathscr{d}f_{y_i}}=P_{y_i}-1\]for the wrong outputs it will be:
\[\frac{\mathscr{dL}_{j_i}}{\mathscr{d}f_{j_i}}=P_{j_i}\space\space for\space(j_i\neq y_i)\]